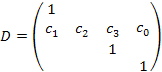Motion and Eddy current correction of diffusion weighted images.

To correct for motion and/or eddy current artefacts in diffusion weighted data, select the corresponding checkboxes in the Diffusion Analysis settings panel. See here .

Transformation model

The transformation model used in motion and eddy current correction of diffusion weighted images is based on an article published in 2004 by G. K. Rohde et. al. titled "Comprehensive approach for correction of motion and distortion in diffusion-weighted MRI". The optimization method however is based on another article from 2001 by T. Netsch et. al. titled "Towards real-time multi-modality 3-D medical image registration" , which uses local correlation as the cost function.

The user has the option to correct for motion and/or eddy current artefacts. Motion can be described by a rigid body transformation, totally six parameters. Eddy current artefacts appear in direction weighted images, and distort the image data mainly along the y-axis, as shown in the article by Rohde et. al. In that article the non-linear distortion was modelled by the following equation:

In our scheme we approximate the distortion by discarding all the second order terms in the equation above. Note alsothat the first coefficient in the equation is unnecessary if motion correction is applied as well, because this parameter corresponds to translation along the y-axis. If we also correct for motion, the total number of parameters is nine. The approximation we have done allows us to describe the transformation as

mapping a voxel x' from the distorted diffusion weighted volume space to the undistorted space of the reference volume. M is the rigid transformation matrix, while D written out is

The benefit of this choice of deformation transformation is the reduced computation time. It has although been shown (Netsch & Muiswinkel, 2004) that comparing this transformation to other more complex transformations does not show any statistically significant difference in the results.

Optimization method

A Gauss Newton optimization algorithm is used with the Local Correlation metric as the cost function, as presented by Netsch et. al. This choice of cost function is what allows us to express our optimization problem as a least squares problem, and thus makes fast computations possible.

View results

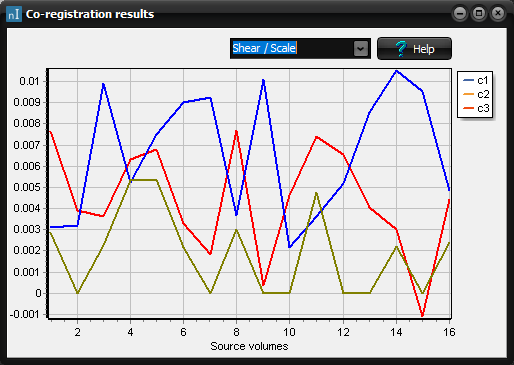
The co-registration results are available through the DTI interaction panel once the co-registration finishes. In the image above, the three graphs correspond to the coefficients in the transformation model for all transformed volumes. Results are also available for translation and rotation parameters as well, given that motion correction is also applied.